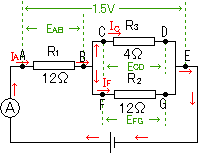
12Ωの抵抗R1,R2 2本と4Ωの抵抗R3 1本を用いて、図1のような回路をつくった。
AE間の電圧は1.5Vを示し、回路の電流計の指針は図2のようであった。
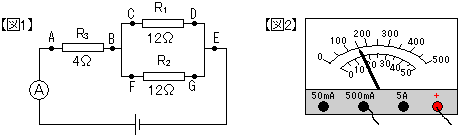
(1) 回路のA点を流れた電流の大きさはいくらか。
(2) AB間の電圧は何Vか。
(3) CD間の電圧は何Vか。
(4) BE間の合成抵抗は何Ωか。
(5) 回路の点Cと点Fを流れた電流の大きさはそれぞれいくらか。
(6) この回路の抵抗R1とR3を入れかえて実験を行った。ただし、AE間の電圧は1.5Vのままとする。
① AE間の合成抵抗は何Ωか。
② AB間の電圧は何Vか。
③ この回路の点A,点C,点Fを流れる電流の大きさはいくらか。
ご質問: かいさん(2004/1/23)
|
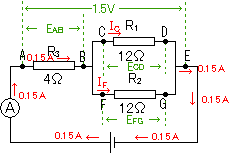
※わかっている数値は、まず、図に書き込んでしまいましょう。
(1)
|
電流計を流れてきた電流はそのままA点に流れこむので、
A点を流れる電流の大きさは電流計の値と同じになります。
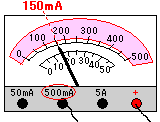
図2を読みとればいいですね。
-端子は500mAのところにつないであるので、めもりは上を読みます。
150mAと読みとれます。A(アンペア)で答えるときは換算しましょう。
1A=1000mAより、150mA=0.15A
参考ページ…回路の電流・電圧>計器の読み方
|
 |
(2)
|
AB間だけでオームの法則を使います。
AB間の抵抗R3を流れる電流は、(1)より0.15A、
抵抗は問題文より4Ω。
AB間の電圧EAB=抵抗R3×電流IA
=4(Ω)×0.15(A)=0.6(V)
参考ページ…オームの法則>基本の公式
|
 |
(3)
R1とR2は並列でつながれているので、CD間にもFG間にも同じ電圧がかかっています。(ECD=EFG)
R1とR2がつくる並列部分をひとつの抵抗と見なしたとき、
R1とR2がつくる並列部分とR3が、AF間の電圧(1.5V)を分け合っています。
この並列部分の電圧を求めればいいですね。R3にかかる電圧は(2)より0.6Vと分かっているので、
CD間の電圧(=FG間の電圧)=AF間の電圧-AB間の電圧
よって1.5(V)-0.6(V)=0.9(V)
参考ページ…回路の電流・電圧>直列回路と並列回路
(4)
R1とR2がつくる並列部分をひとつの抵抗と見なしたときの抵抗値を求めます。
BC間・DE間には抵抗がないので、BE間の電圧はCD間の電圧と同じです。(3)より0.9Vだとわかっています。
また、Bを流れる電流は0.15Aなので、BE間でオームの法則を使います。

参考ページ…オームの法則>基本の公式
【別解】並列回路の合成抵抗の求め方の公式を習っていれば使います。
BE間の合成抵抗をEBEとして、
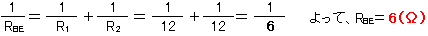
参考ページ…オームの法則>電圧電流の分け方・合成抵抗(参考)
(5)
点Cを流れた電流ICは、R1についてオームの法則を使います。
(3)より、R1(12Ω)には0.9Vの電圧がかかっているので、
電流IC=電圧÷抵抗=0.9(V)÷12(Ω)=0.075(A)
R2(12Ω)についても同じく0.9(V)の電圧がはたらいていて、抵抗値も12Ωで同じなので、点Fにも0.075Aの電流が流れるはずです。
それらがE点で合流して0.075(A)+0.075(A)=0.15(A)の電流となります。
※R1もR2も同じ抵抗値なので、電流が半分に分かれて流れると考えてもいいです。
0.15(A)÷2=0.075(A)
(6)
|
①
R1・R2・R3をひとつの抵抗と見なした場合の抵抗値を求めます。
R3とR2については並列回路の合成抵抗の公式を使うと早いです。
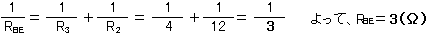
並列部分とR1は直列につながっているので、抵抗値は足し算できます。
よって、合成抵抗R=R1+RBE=12(Ω)+3(Ω)=15(Ω)
参考ページ…オームの法則>電圧電流の分け方・合成抵抗(参考)
②
回路全体に流れる電流を求めます。
AE間の電圧1.5Vと合成抵抗15Ωについてオームの法則を使うと、
電流=電圧÷抵抗=1.5(V)÷15(Ω)=0.1(A)
R1(12Ω)には0.1A流れていることがわかったので、オームの法則より、
AB間の電圧EAB=抵抗×電流=12(Ω)×0.1(A)=1.2(V)
|
 |
③
A点を流れるのは②より0.1Aです。
②より、並列部分にかかる電圧は1.5(V)-1.2(V)=0.3(V)
R3(4Ω)に0.3Vの電圧がかかっているので、C点を流れる電流ICはオームの法則より、
IC=電圧÷抵抗=0.3(V)÷4(Ω)=0.075(A)
IA(0.1A)が枝分かれしてICとIFになるので、F点を流れる電流は、
IF=IA-IC=0.1(A)-0.075(A)=0.025(A)
【別解】
並列回路の合成抵抗の公式を習っていなくても解くことができますが、考え方が少々難しくなります。
並列部分について電流の流れ方を考えてみましょう。
R2はR3より抵抗が3倍大きいので、電流はR3にR2の3倍流れます。
IC=3IF
R1に流れる電流IAが枝分かれしてICとIFとなるので、
IA=IC+IF これに先ほどの「IC=3IF」を代入して IA=3IF+IF=4IF(IAはIFの4倍)
R1とR2は同じ抵抗値のはずですが、流れる電流はR1が4倍多いことがわかりました。
ということは、R1にはR2(並列部分)の4倍の電圧がかかっていることになります。
R1と並列部分でAE間の電圧(1.5V)を4:1で分け合っているので、
並列部分(R2やR3)には1.5(V)÷(4+1)=0.3V、R1にはその4倍の1.2Vの電圧がかかっていますね。
R1に流れる電流(点Aを流れる電流)はオームの法則より、電圧÷抵抗=1.2(V)÷12(Ω)=0.1(A)
となり、これが全体の電流となるので、全体の電圧(1.5V)とオームの法則より、
全体の抵抗(合成抵抗)=全体の電圧÷全体の電流=1.5(V)÷0.1(A)=15(Ω)
となります。
いっぽう、並列部分(R2やR3)には0.3Vの電圧がかかっていました。
ここでもオームの法則を使って点C・Fに流れる電流を求めることができます。
R3(4Ω)にかかる電圧は0.3Vなので、IC=電圧÷抵抗=0.3(V)÷4(Ω)=0.075(A)
R2(12Ω)にかかる電圧は0.3Vなので、IF=電圧÷抵抗=0.3(V)÷12(Ω)=0.025(A)
答え
|
(1)150mAまたは0.15A
(2)0.6V
(3)0.9V
(4)6Ω
(5)点C-0.075A 点F-0.075A
(6)①15Ω ②1.2V
③点A-0.1A,点C-0.075A,点F-0.025A
|
問題データベース目次へ



