このページでは、余裕があれば知っておくと便利なことを紹介します。
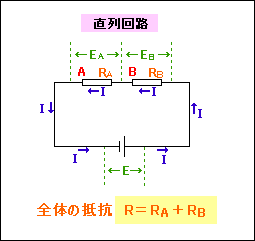
直列回路での電圧の分け方
直列回路では、2つの抵抗が電源の電圧を分け合います。
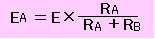
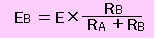
直列回路では、回路のどこでも同じ大きさの電流が流れています。
抵抗Aでも抵抗Bでも同じ大きさの電流が流れていることと、オームの法則を使って導き出せます。
|
|
これは、電源の電圧をRA:RBで分け合っているということです。
EA:EB=RA:RB
たとえばAが2Ω、Bが3Ωで、電源が10Vなら、電圧はAとBで2:3で分け合うので、抵抗の小さいAには4V、抵抗の大きいBには6Vかかるというわけです。
電源の電圧とそれぞれの抵抗値がわかっていれば、それぞれの抵抗にどれだけ電圧がかかっているか知ることができます。
並列回路での電流の分け方
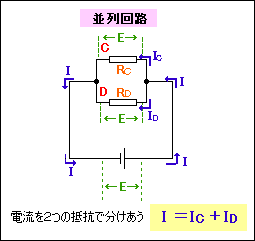
並列回路では、2つの抵抗が全体の電流を分け合います。
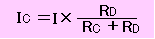
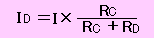
並列回路ではどの抵抗にも電源と同じ電圧がかかっています。
このことと、オームの法則を使って導き出せます。
|
|
これは、全体の電流をCとDでRD:RCで分け合っているということです。
IC:ID=RD:RC
たとえば、Cが20Ω、Dが30Ωで、全体の電流が5Aなら、電流はCとDで3:2で分け合うので、抵抗の小さいCには3A、抵抗の大きいDには2A流れるというわけです。
全体の電流とそれぞれの抵抗値がわかっていれば、それぞれの抵抗にどれだけ電流が流れているか知ることができます。
並列回路の合成抵抗
並列回路で全体の抵抗を求める公式があります。
|
Rを全体の抵抗とすると、
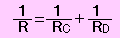
の関係からRが求められます。
I=IC+IDとオームの法則を使って導き出せます。
|
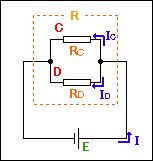
|
それぞれの抵抗値がわかっていれば、全体の抵抗が求められます。
抵抗が3個以上直列や並列につながれていても、順序よく求めれば全体の抵抗が求められます。
ひとつやってみましょう。
|
【例題3】下の図で、全体の抵抗を求めよ。
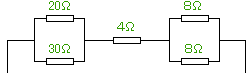
|
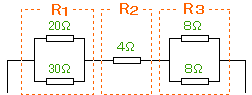
右図のように考えるとカンタンです。
R1とR2とR3が直列につながっていることになりますね。R1を計算すると12Ω 計算式はこちら
R3を計算すると4Ω 計算式はこちら
よって、全体の抵抗は
12(Ω)+4(Ω)+4(Ω)=20(Ω)
となります。
|
|
***************************************************************************************
合成抵抗の公式は求めるRが分母にあるので、つい計算ミスしがちです。
これについては、上の公式を変形した別の公式と、覚え方のアイディアをいただきました。Mさん、ありがとうございました。
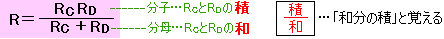
【注意】
抵抗が2個並列の場合のみ使えます。3個以上並列になっている場合は

を使ってください。(逆数…1をその数で割ったもの)
導線の長さと断面積
中学では導線の抵抗はない(抵抗値は0Ω)としていますが、実は導線にも抵抗があります。
習わない学校がほとんどだと思いますが、もし習っていたら参考にしてください。
同じ金属でできている導線は、長くて細いほど抵抗が大きくなります。
水路でも、長い水路はあちこちに引っかかる可能性が大きくなって水が流れにくくなり、
太ければ水がたくさん流れていきやすいので、「水路→導線」「水→電流」とするとイメージしやすいですね。
よって、これを公式化すると

となります。
※12Ωの導線の長さが3倍に、断面積が2倍になったときの抵抗値は 12×3÷2=18(Ω) となるわけです。
このことから、長さや断面積をかけたり割ったりすると抵抗が求められる「もととなる抵抗値」を決めておくと便利ですね。
金属によってこの「もととなる抵抗値」は決まっていて、体積抵抗率と呼ばれます。

※銅(ρ=1.55×10-8Ω・m)で作った5m、5mm2(=5×10-6m2)の導線の抵抗は
1.55×10-8(Ω・m)×5(m)÷5×10-6(m2)=1.55×10-2(Ω)=0.0155(Ω)
となります。とても小さい抵抗値ですね。
top
> 電流と磁界 > オームの法則 > 電圧・電流の分け方 合成抵抗(参考)





