|
恾偵帵偟偨憰抲傪巊偭偰巁壔摵乮嘦乯暡枛傪擖傟偨僗僥儞儗僗偺嶮傪僈儔僗娗偵擖傟丆壓偐傜壛擬偟側偑傜悈慺傪捠偡偲丆師偺傛偆側娨尦斀墳偑婲偙偭偰摵偑惗偠傞丅
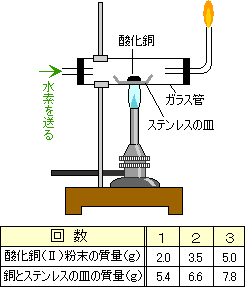
丂丂丂丂丂丂丂CuO+H2仺Cu+H2O 巁壔摵乮嘦乯偺幙検傪偄傠偄傠偵曄偊偰幚尡偟丆壛擬屻偺僗僥儞儗僗偺嶮傪傆偔傔偨摵偺幙検傪挷傋偨傜丆昞偺傛偆偵側傝傑偟偨丅師偺奺栤偄偵摎偊側偝偄丅 偛幙栤丗 keiichiro偝傫乮2003/2/15乯 |
 |
|
栤侾
巁壔摵偑悈慺偵傛偭偰娨尦偝傟偨偲偄偆幚尡偱偡偹丅壔崌暔偺幙検偺斾偼堦掕偱偁傞偙偲傪巊偄傑偡丅娭楢儁乕僕
偙偺応崌偺巁壔摵偵傆偔傑傟傞丂巁壔摵丗摵丂偺幙検斾傪媮傔偰傒傑偟傚偆丅
堦掕検偺巁壔摵偐傜偱偒傞摵偺幙検偝偊傢偐傟偽丄僗僥儞儗僗偺嶮偺幙検偼堷偒嶼偱傢偐傝傑偡偹丅
|
昞傪尒偰傒傑偡丅
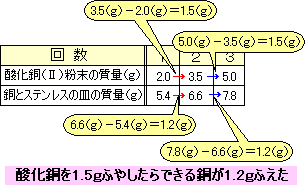
乽巁壔摵偺幙検傪1.5倗傆傗偟偨傜丄娨尦屻偺摵偑1.2倗傆偊偨乿偲偄偆寢壥偱偟偨丅 巁壔摵1.5倗偵懳偟偰摵偺妱崌偼1.2倗偱偁傞偲偄偊傑偡偹丅 巁壔摵丗摵亖1.5乮倗乯丗1.2乮倗乯亖5丗4 巁壔摵5偵懳偟偰丄摵偼4偺妱崌偲傢偐傝傑偟偨丅 |
 |
偳偺夞悢偺僨乕僞偱傕傛偄偺偱丄偦偺偲偒偺巁壔摵偵懳偡傞摵偺幙検傪媮傔偰傒傑偟傚偆丅
偙偙偱偼侾夞栚偺乽巁壔摵2.0倗偺偲偒丄摵偲僗僥儞儗僗偺嶮偼5.4倗乿偲偄偆僨乕僞傪巊偭偰偄偒傑偡丅
巁壔摵2.0倗偐傜偱偒傞摵冊倗偼丂巁壔摵丗摵亖2.0乮倗乯丗冊乮倗乯亖5丗4丂丂斾椺幃偺夝偒曽
偙傟傪夝偔偲丂冊亖1.6乮倗乯丂偲側傝傑偡丅摵偑1.6倗偩偲傢偐偭偨偺偱丄僗僥儞儗僗偺嶮偼
丂丂5.4乮倗乯亅1.6乮倗乯亖3.8乮倗乯丂丂傛偭偰丄僗僥儞儗僗偺嶮偺幙検偼3.8倗偱偡偹丅丂娭楢儁乕僕
栤俀
巁壔摵丗摵亖5丗4丂偑栤侾傛傝媮傑偭偰偄傞偺偱丄栤俀偼妝彑偱偡丅
巁壔摵4.0倗偺偲偒偵偱偒傞摵偺幙検傪倷倗偲偡傞偲丄
巁壔摵丗摵亖4.0乮倗乯丗倷乮倗乯亖5丗4丂偙偺斾椺幃傪夝偔偲丄倷亖3.2乮倗乯
傛偭偰丄惗偠傞摵偺幙検偼3.2倗偲側傝傑偡丅
栤俁
偙偺僞僀僾偺栤戣偱乽斀墳偟側偐偭偨幙検乿傪媮傔傞偲偒偼斀墳偵娭學偟偨巁慺偺幙検偵拲栚偟傑偡丅
傑偢丄壗倗偺巁慺偑偆偽傢傟偨偐寁嶼偟傑偟傚偆丅
10倗偺僗僥儞儗僗嶮偵偺偭偰偄傞暔幙偺幙検偼丂10乮倗乯亅3.8乮倗乯亖6.2乮倗乯丂偺偼偢偱偡偹丅
7.0倗偺巁壔摵偑6.2倗偺乽摵偲巁壔摵乿偵側偭偨偺偱偡偐傜丄
偆偽傢傟偨巁慺偺幙検偼丂丂7.0乮倗乯亅6.2乮倗乯亖0.8乮倗乯丂偱偡丅
巁壔摵偺幙検亖摵偺幙検亄偆偽傢傟偨巁慺偺幙検
偱偡偐傜丄巁壔摵俆偵懳偟偰摵偑係偱偁傞側傜丄巁慺偺幙検偺妱崌偼侾偱偡偹丅丂巁壔摵丗摵丗巁慺亖5丗4丗1
0.8倗偺巁慺偑倸倗偺摵偲寢傃偮偄偰偄偨偲偡傞偲丄丂摵丗巁慺亖倸乮倗乯丗0.8乮倗乯亖4丗1
偙偺斾椺幃傪夝偔偲丂倸亖3.2乮倗乯丂偲側傝傑偡丅6.2倗偺偆偪丄摵偑3.2倗側偺偱丄巆傝偼斀墳偟側偄偱巆偭偨巁壔摵偱偡丅
6.2乮倗乯亅3.2乮倗乯亖3.0乮倗乯丂傛偭偰丄3.0倗偺巁壔摵偑巆傝傑偡丅娭楢儁乕僕
摎偊
|
栤侾丂3.8倗 |
仸巁壔摵乮嘦乯偲偄偆偺偼拞妛偱廗偆崟偄巁壔摵乮CuO乯偺偙偲偱丄惓幃偵偼巁壔戞擇摵偲偄偄傑偡丅
偪側傒偵巁壔摵乮嘥乯偱偁傞巁壔戞堦摵乮Cu2O乯偼愒怓偺寢徎偺暡枛偱偡丅