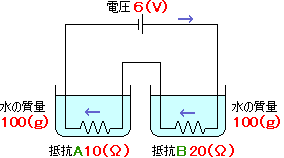
 例として、10Ωと20Ωの抵抗を直列につないで、それぞれ100gの水につけ、全体に6Vの電圧をかけて50分間電流を流したときの、それぞれの抵抗の発熱量と水の上昇温度を考えてみましょう。 例として、10Ωと20Ωの抵抗を直列につないで、それぞれ100gの水につけ、全体に6Vの電圧をかけて50分間電流を流したときの、それぞれの抵抗の発熱量と水の上昇温度を考えてみましょう。
抵抗の発熱量はすべて水の温度上昇に使われたものとします。 | |
| 回路を流れる電流を求めてみます。直列回路なので、電流の大きさは回路のどこでも同じ です。全体の抵抗は R=10(Ω)+20(Ω)=30(Ω) 電源の電圧は6Vなので、オームの法則より、 | |
| 抵抗Aについて | 抵抗Bについて |
|
抵抗Aにかかる電圧を求めてみましょう。 オームの法則より、電圧=抵抗×電流 EA=RA×I =10(Ω)×0.2(A)=2(V) 抵抗Aにかかる電圧は2V ※EA:EB=RA:RB=1:2で求めてもOK。 |
抵抗Bにかかる電圧を求めてみましょう。 オームの法則より、電圧=抵抗×電流 EB=RB×I =20(Ω)×0.2(A)=4(V) 抵抗Bにかかる電圧は4V ※EA:EB=RA:RB=1:2で求めてもOK。 |
|
抵抗Aの電力を求めてみましょう。 電力=電圧×電流 PA=EA×I=2(V)×0.2(A)=0.4(W) 抵抗Aの電力は0.4W |
抵抗Bの電力を求めてみましょう。 電力=電圧×電流 PB=EB×I=4(V)×0.2(A)=0.8(W) 抵抗Bの電力は0.8W |
|
抵抗Aの50分間の発熱量を求めてみます。 発熱量=0.24×電力×秒数 (50分=3000秒) QA=0.24×0.4(W)×3000(秒) =288(cal) 50分間の抵抗Aの発熱量は288cal |
抵抗Bの50分間の発熱量を求めてみます。 発熱量=0.24×電力×秒数 (50分=3000秒) QB=0.24×0.8(W)×3000(秒) =576(cal) 50分間の抵抗Bの発熱量は576cal |
|
抵抗Aの50分間の水の上昇温度を求めてみましょう。 発熱量=水の質量×上昇温度 (水の質量は100g) TA=288(cal)÷100(g)=2.88(℃) 50分間の抵抗Aによる水の上昇温度は |
抵抗Bの50分間の水の上昇温度を求めてみましょう。 発熱量=水の質量×上昇温度 (水の質量は100g) TB=576(cal)÷100(g)=5.76(℃) 50分間の抵抗Bによる水の上昇温度は |
直列回路では抵抗が大きいほど、発熱量や水の上昇温度が大きくなりそうですね。
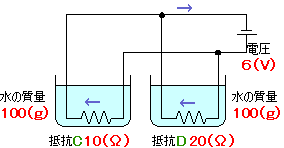 例として、10Ωと20Ωの抵抗を並列につないで、それぞれ100gの水につけ、全体に6Vの電圧をかけて50分間電流を流したときの、それぞれの抵抗の発熱量と水の上昇温度を考えてみましょう。
例として、10Ωと20Ωの抵抗を並列につないで、それぞれ100gの水につけ、全体に6Vの電圧をかけて50分間電流を流したときの、それぞれの抵抗の発熱量と水の上昇温度を考えてみましょう。