料理用の電熱器などは電熱線から発生した熱量を使っていろいろなものをあたためています。
電熱線を水につけたときの水温の変化について考えてみましょう。
水が得た熱量の公式を忘れてしまった人はこちらで復習してください。なお、ここでは抵抗器の図記号は以前のまま使っています。

電熱線の発熱量で水をあたためる

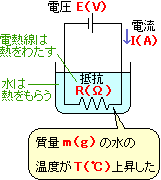
E（V）の電圧をかけ、I（A）の電流を t（秒間） 流した電熱線の発熱量Q（cal）は Q（cal）＝0.24×E（V）×I（A）×ｔ（秒） P（W）の電熱線に電流を t（秒間） 流した電熱線の発熱量Q（cal）は Q（cal）＝0.24×P（W）×ｔ（秒）
m（ｇ）の質量の水の水温がT（℃）上昇したとき、 水が得た熱量は 熱量（cal）＝m（ｇ）×T（℃）

もし、電熱線の発熱量がすべて水温の上昇に使われたなら、

電熱線の発熱量＝水が得た熱量

なので、　0.24×E×I×ｔ ＝m×T　または　0.24×P×ｔ ＝m×T　が成り立ちます。

※電熱線の発熱量Qを求めるための数値は、電圧や電流以外に抵抗値と電流、抵抗値と電圧、といった数値で与えられていたりします。
抵抗値が出てきたときはオームの法則を使って、電圧と電流を求めましょう。

オームの法則はこちらで復習してください。

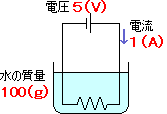
【例題７】 電熱線に5Vの電圧をかけて１Aの電流を 5分間流したら、100ｇの水の温度は何℃ 上がるか。電熱線の発熱量はすべて水温 の上昇に使われたものとする。

電熱線の発熱量はQ（cal）＝0.24×5（V）×１（A）×300（秒）＝360（cal）　　※5分＝5×60（秒）＝300（秒）
この熱量が水に与えられた熱量なので、　電熱線の発熱量＝水が得た熱量　となります。
水の質量はm＝100（ｇ）なので、　360（cal）＝100（ｇ）×T（℃）　　これをTについて解くと、　T＝3.6（℃）

答えは3.6℃上がる。

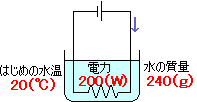
【例題８】 200Wの電熱線に電流を流し、20℃・240ｇの 水をあたためた。この水が沸騰するには 何分何秒電流を流し続ければよいか。電熱線の 発熱量はすべて水温の上昇に使われたものとする。

20℃の水が100℃になるには　100（℃）−20（℃）＝80（℃）　T＝80（℃）上昇したことになります。
240ｇの水の得た熱量＝240（ｇ）×80（℃）　　これを電熱線からもらえばいいですね。ｔ 秒通電したとして、
電熱線の発熱量＝水が得た熱量　より、　0.24×200（W）×ｔ（秒）＝240（ｇ）×80（℃）
これを t について解くと、ｔ＝400（秒）　　１分＝60秒なので、　400÷60＝6…40

答えは6分40秒電流を流す。

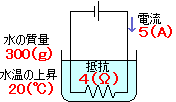
【例題９】 ４Ωの電熱線に５Aの電流を５分間流したら、 300ｇの水の温度が20℃上がった。 逃げてしまった熱量は何calか。

電熱線の発熱量を求めるには電圧の値を求めないといけませんね。
オームの法則より、電圧E＝R×I＝4（Ω）×5（A）＝20（V）
発熱量Q（cal）＝0.24×20（V）×5（A）×300（秒）＝7200（cal）　　※5分＝5×60（秒）＝300（秒）

一方、水が得た熱量も求めてみます。水の質量はm＝300（ｇ）、上昇温度はT＝20（℃）なので、
水の得た熱量＝300（ｇ）×20（℃）＝6000（cal）

逃げてしまった熱量＝発熱量−水の得た熱量＝7200（cal）−6000（cal）＝1200（cal）

答えは1200cal逃げた。

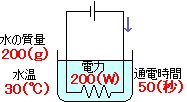
【例題10】 200Wの電熱線に50秒間電流を流した。 30℃・200ｇの水は何℃になるか。 電熱線の発熱量はすべて水温の上昇に 使われたものとする。

電熱線の発熱量はQ（cal）＝0.24×200（W）×50（秒）＝2400（cal）
この熱量が水に与えられた熱量なので、　電熱線の発熱量＝水が得た熱量　となります。
水の質量はm＝200（ｇ）なので、上昇した水温をT℃として、
2400（cal）＝200（ｇ）×T（℃）　　これをTについて解くと、　T＝12（℃）
もとの水温は30℃なので、上昇分を足して　30（℃）＋12（℃）＝42（℃）

答えは42℃

※求める水温をχ℃として、　0.24×200（W）×50（秒）＝200（ｇ）×（χ−30）（℃）　といきなり方程式をつくってもいいですね。

top 　>　電流と磁界　>　電力・ジュールの法則　>　水の温度変化（参考）